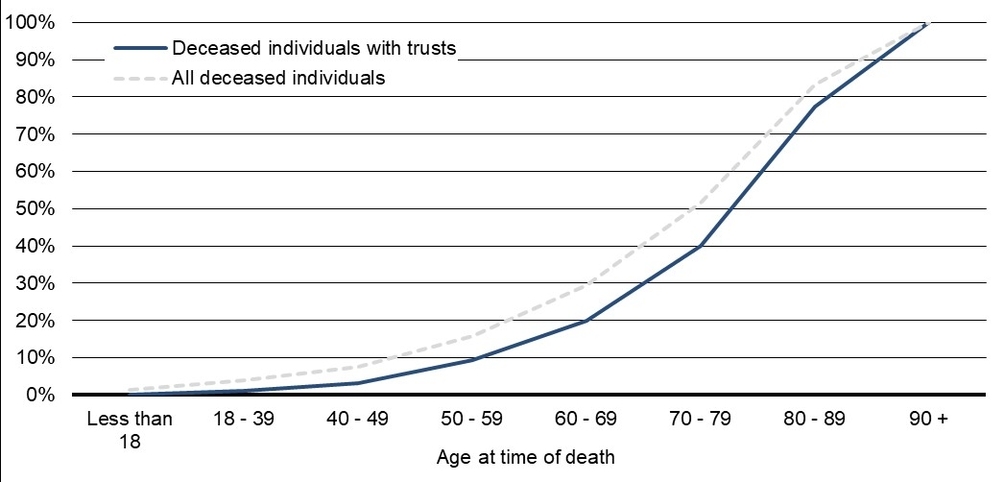
Cumulative Distributions by Age
Cumulative distributions are a fundamental concept in probability theory and statistics. The cumulative distribution function (CDF) of a real-valued random variable, evaluated at a certain point, is the probability that the variable will take a value less than or equal to that point.
In the context of age, cumulative distributions can be used to analyze various phenomena. For instance, they can be used to study the distribution of ages in a population, the age at which certain milestones are reached, or the lifespan of individuals in a population.
Understanding Cumulative Distributions
The CDF is a right-continuous monotone increasing function, satisfying certain properties. For a continuous distribution, the CDF gives the area under the probability density function from negative infinity to the given point. The probability density function of a continuous random variable can be determined from the CDF by differentiating.
Cumulative Distributions by Age in Populations
In demographics, cumulative distributions by age can be used to create age pyramids, which graphically represent the age structure of a population. The x-axis represents age groups, while the y-axis represents the number or percentage of individuals in each age group. The shape of the pyramid can provide insights into the population’s growth rate, life expectancy, and age distribution.
Cumulative Distributions in Lifespan Analysis
In lifespan or survival analysis, the CDF can be used to represent the probability of an individual surviving up to a certain age. This can be particularly useful in fields like medicine or reliability engineering. For instance, the Weibull distribution, a specific type of cumulative distribution function, is commonly used in failure analysis.
Cumulative Age Distributions in Geology
In geology, the Cumulative Age Distribution (CAD) is a discrete step-function with sorted detrital age measurements on the x-axis and their respective ranks on the y-axis. This can be used to analyze the age distribution of rock particles in a sample, providing insights into the geological history of the area.
Age Standardization in Epidemiology
In epidemiology, cumulative distributions by age are used in age standardization, a technique used to eliminate the effect of age when comparing disease rates between different populations. The cumulative rate is the sum of the age-specific rates over each year of age from birth to a defined upper age limit.
Conclusion
Cumulative distributions by age are a powerful tool in various fields, from demographics to geology to epidemiology. They provide a way to analyze and visualize age-related data, allowing for meaningful comparisons and insights..